안녕하세요 오늘은 최근 실무를 하면서 처음 접해본 내용에 대해서 글을 작성해 보려고 합니다.
최근에 Plant 설계를 진행하면서 Pipe나 전기배선 선반 구조물을 지지하는 작은 기둥을 검토하는 중에 Paving type support에 대해서 접하게 되었습니다. 이러한 형태의 기초는 Paving위에 pedestal을 설치하여 기초의 역할을 하게 됩니다. 즉, 별도의 기초를 시공하지 않고 paving이 기초역할을 하게 되는 것입니다.
이러한 형태의 기초를 설계할때 기본적으로 알고 있어야할 개념이 상대강성반경(Radius of Relative Stiffness)입니다.
그렇다면 이제부터 개념과 수식에 대해서 알아보겠습니다.
"Radius of Relative Stiffness"는 판(plate) 구조물의 거동을 해석할 때 매우 중요한 개념입니다. 특히 콘크리트 포장, 지반 위의 슬래브, 연속 기초, 기초판 등에서 하중이 작용할 때 판이 얼마나 멀리까지 하중을 전달할 수 있는가를 평가하는 데 사용됩니다.

ℓ 값은 판이 지반 위에서 하중을 수평 방향으로 전달할 수 있는 거리를 나타냅니다.
ℓ이 클수록 판이 하중을 넓게 퍼뜨릴 수 있음을 의미합니다. 즉, 더 유연하거나 지반이 단단할수록 ℓ이 작아지고, 판이 더 두껍거나 강성이 크면 ℓ이 커집니다.
위의 수식을 하나씩 뜯어보면 다음과 같이 탄성이론에 따라 결과를 유도할 수 있습니다.
Radius of Relative Stiffness의 의미는 기초판 혹은 슬래브와 지반의 상대적인 강성비를 의미하는 것을 위에서 설명드렸습니다.
그렇다면 콘크리트 슬래브의 강성과 지반의 강성을 각각 알아보겠습니다.
슬래브의 강성은 결론적으로 보면 아래와 같습니다.

기본 가정은 Kirchhoff-Love Plate Theory에 따라 다음과 같습니다.
- 슬래브는 등방성 탄성체이며, 두께는 평면 치수에 비해 매우 얇다.
- 굽힘 시, 판의 중립면 상하에서 수직선은 평면을 유지하며 휘어짐 (전단 변형 무시).
- 하중은 슬래브 표면에 수직으로 작용한다 (정적 하중 기준).
이와 같은 가정으로 휨강성을 구하게 될텐데 우선 보(beam)이라고 생각하고 1방향에 대해서만 고려해보겠습니다.

위의 식은 재료역학에서 확인할 수 있습니다. 휨응력과 곡률의 관계는 기본적인 내용이므로 설명을 별도로 하지 않겠습니다!
모멘트를 구하기 위해서 면적에 대해서 적분을 하면 아래와 같습니다.

그러므로 1방향 휨해석인 보와 같은 구조물에서는 다음과 같은 결론에 도달합니다.

하지만 슬래브는 2방향 판요소입니다. 이제 2방향에 대해서 설명해보겠습니다.
탄성이론에서 응력-변형률 관계는 다음과 같습니다.

이것은 Hook's law를 3차원으로 확장했을 때 자명하게 알 수 있습니다. 푸아송 효과를 고려하게 됩니다. 혹시 탄성이론에 대해서 잘 모르겠다면 아래의 유튜브를 한번 확인해보시고 기본적인 탄성이론에 대해서 공부하는 시간을 가지는 것도 좋을 것 같습니다.
https://www.youtube.com/watch?v=sXlngu0S6C8
위의 변형률을 통해서 응력표현하면 다음과 같습니다.

1방향 모멘트를 구할때 처럼 같은 방식을 통해서 산정하면 다음과 같습니다.
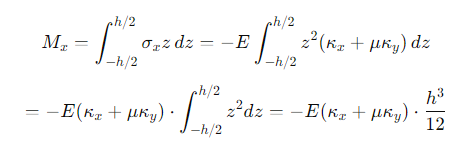
마찬가지로 y방향도 다음과 같습니다.
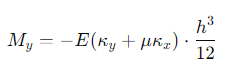
최종적으로 다음과 같아집니다.
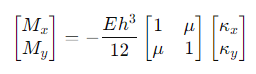
그러므로 휨강성은 다음과 같아집니다.

또한 지반의 강성은 k값으로 설정되어 있습니다. 그래서 다음과 같이 표현됩니다.
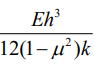
또한, 위의 값은 길이의 4제곱인것을 확인할 수 있습니다. 그러므로
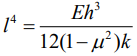
다음과 같게 표현할 수 있습니다.
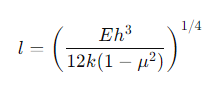
최종적으로는 Radius of Relative Stiffness를 위의 식으로 표현하게 됩니다.
Radius of Relative Stiffness에 대해서 알아보았습니다. Radius of Relative Stiffness의 활요은 다음과 같이 여러가지가 있습니다.
- Westergaard의 콘크리트 포장 해석: 하중 위치(내부, 모서리, 가장자리)에 따른 응력 계산에 사용됨.
- 슬래브 기초 설계: 기초판의 하중 분산 범위 판단.
- 플레이트 온 서브그레이드 모델링: FEM 해석 시 mesh 크기 및 범위 설정 참고.
- 접촉 응력, 침하량 분포 등 계산 시 기초 길이와 비교.
실제로 이번 프로젝트에서도 Westergaard의 콘크리트 포장 해석에 해당 개념이 나와서 공부하게 되었습니다.
다음에는 Westergaard의 수식에 대해서도 알아보겠습니다.
지금까지 글을 읽어 주셔서 감사합니다😊
'콘크리트' 카테고리의 다른 글
| 비틀림 공식의 유도 (0) | 2024.11.19 |
|---|---|
| 전단 메커니즘의 이해-2편 : 전단 철근이 보강된 보 (0) | 2024.09.30 |
| 전단 메커니즘의 이해-1편 : 전단 철근이 없는 부재에 대하여 (0) | 2024.09.22 |
| 기둥의 좌굴과 장주의 설계(세장비, 확대휨모멘트, 오일러 좌굴하중) (0) | 2024.09.18 |
| 2축 휨을 받는 기둥: 실제 기둥은 대부분 2축 휨을 받는다. (0) | 2024.09.13 |



